和田先生
和田先生
従って,初期値問題が解けることになります.
初期値問題の特殊解
強制振動と時系列波形
こっしー君
式(45),(50),(51)は複雑で,ここから振動の様子をうかがい知ることは,簡単ではありませんので,各パラメータに数値を代入して考えてみます.用いるパラメータは,以前の「振動現象の,自己と“ちょっと変わった”他者」で用いたものを使います.すなわち,固有角振動数  ,減衰比(減衰係数比)
,減衰比(減衰係数比) ,対象物の質量
,対象物の質量  を以下の場合について考えます.
を以下の場合について考えます.
 (52)
(52)
 (53)
(53)
 . (54)
. (54)
これは,前回の式(34)より,


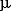
 (55)
(55)
 (56)
(56)
であることを表します.
このとき,外力の角振動数) を以下の場合について考えます.
を以下の場合について考えます.
(I)
(II)
(III)
(IV)
(V)
初期条件は,同様に(式(46)),

とします.
そして,以前の(「振動現象の,自己と“ちょっと変わった”他者」)同様,各条件下での変位) の時系列変動を示します.
の時系列変動を示します.
各角振動数 を持つ周期的外力
を持つ周期的外力 ) の力学系への影響が,系の振動にどのように表れるかがわかります.系の持つ固有角振動数は,いわば,自己の個性のようなものであると考えると,自己以外の他者の働きかけが,自己にどのような影響を及ぼすのかが分かるような気がしてきます.
の力学系への影響が,系の振動にどのように表れるかがわかります.系の持つ固有角振動数は,いわば,自己の個性のようなものであると考えると,自己以外の他者の働きかけが,自己にどのような影響を及ぼすのかが分かるような気がしてきます.
これは,前回の式(34)より,
であることを表します.
このとき,外力の角振動数
(I)
(II)
(III)
(IV)
(V)
初期条件は,同様に(式(46)),
とします.
そして,以前の(「振動現象の,自己と“ちょっと変わった”他者」)同様,各条件下での変位
各角振動数
こっしー君
和田先生
ありがとうございます.特徴をまとめてください.
こっしー君
共通して言えることは,よく見ると初期のうちで(15-20 ms あたりまで),式(45)の第1項にあたる自由振動項がみられるようにも思いますが,後半以降では減衰して見られなくなります.
次に,強制振動項ですが,(I)では,のこぎり波の成分がみられます.ここで特徴的なのは,高周波成分がみられることです.これは,外力をのこぎり波としたことにより,不連続点を持つことになり,この影響によるものであると考えます.(II)でも,よくみるとのこぎり波の影響がみられるようにも思いますが,波形は,共振していると考えられる(III)に近くなっています.
のこぎり波入力における出力波は,低周波((I))では不連続点の影響が顕著になり,三角波との相違が現れますが,共振状態近傍より大きな振動を与えると,波形は三角波入力の場合とよく似てくると考えます.
次に,強制振動項ですが,(I)では,のこぎり波の成分がみられます.ここで特徴的なのは,高周波成分がみられることです.これは,外力をのこぎり波としたことにより,不連続点を持つことになり,この影響によるものであると考えます.(II)でも,よくみるとのこぎり波の影響がみられるようにも思いますが,波形は,共振していると考えられる(III)に近くなっています.
のこぎり波入力における出力波は,低周波((I))では不連続点の影響が顕著になり,三角波との相違が現れますが,共振状態近傍より大きな振動を与えると,波形は三角波入力の場合とよく似てくると考えます.
和田先生
今回は,この辺にしておきましょう.機会があれば次回は,外力が周期関数ですが,正弦波の単純な組み合わせでは表せない場合の次の例,矩形波についてお話しいたします.この場合も,フーリエ級数展開によって外力波形を表現します.実は,我々は,この矩形波入力を用いた場合について研究をしています.
この記事と合わせて読みたいページ
和田先生のプロフィール

TMCシステムの研究責任者.電子情報通信学会の会員.
電気接点の劣化現象などに関する論文を多数執筆.
プライベートでは,ギター演奏・料理・読書と幅広い趣味を持つ.
こっしー君のプロフィール

TMCシステムの研究担当者.電子情報通信学会の会員.
得意分野は数学と機械工学.
趣味は読書.特技はペン習字.
※記事の内容に関するご質問などがございましたら、お問い合わせからご連絡いただくか、もしくはコメント欄↓にご記入いただければと思います。後日、担当者よりご連絡させていただきます。




















