【こっしーの研究レポート4】振動する薄板のモデリング(1質点近似)

振動によりコネクタなどが劣化する場合，振動数や減衰の違いにより，劣化の速さなどが異なる可能性があります．そのため，ハンマリング加振機構[1]を用いて薄板を加振したときに，薄板がどのように振動するのかを理解しておくことは，ハンマリング加振機構により実験を行う際に有用となります．そこで，ハンマリング加振機構を用いて，薄板を加振したときの振動を数理モデル化して計算することを試みています．今回は，薄板上の1点を質量とばねと減衰器からなる1自由度振動系とみなして，1質点近似したモデルを説明します．

モデル1: 角振動数が一定の減衰波

質量を $m$ ，粘性減衰係数を $c$ ，ばね定数を $k$ ，時刻を $t$ ，静的釣合の位置からの変位を $x$ ，加振時に与えられる力積を $I_0$ ，ディラックのデルタ関数を $\delta(t)\,$ とします． $t=0\;\;{\rm s}$ において振動が開始するとします．加振時に薄板へ加わる力がインパルス入力であるとしますと，運動方程式は，

$m\ddot{x}(t)+c\dot{x}(t)+kx(t)=I_{0}\;\;\delta (t)$

となります[2]．ここで，

$\lim _{t\to -0}\dot{x}(t) =0$

としますと，

$\lim _{t\to +0}m\dot{x}(t)-\lim _{t\to -0}m\dot{x}(t) =I_{0}$

より，

$\lim _{t\to +0}m\dot{x}(t) =I_{0}$ ．

従って，

$\lim _{t\to +0}\dot{x}(t)=\Large\frac{I_{0}}{m}$

となります．よって初期条件を，

$x(+0)=0\,,\;\;\dot{x}(+0) =\Large\frac{I_{0}}{m}$

として，

$m\ddot{x}(t)+c\dot{x}(t)+kx(t)=0$

を解けばよいことになります．これを【和田先生のなるほどゼミナール2】振動現象をつむぐ，中学校の数学2から【和田先生のなるほどゼミナール5】振動現象をつむぐ，中学校の数学5の内容にしたがって解きますと，

$x(t)=Ae^{-\gamma t}\sin \omega t$ 　　　(1)

の形で解が得られます．ここで，

$A={\Large\frac{2I_{0}}{\sqrt{4mk-c^{2}}}}$ ， $\gamma ={\Large\frac{c}{2m}}$ ， $\omega =\Large\frac{\sqrt{4mk-c^{2}}}{2m}$

です．

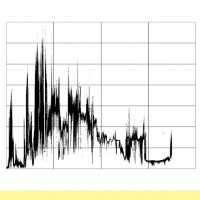
実際にハンマリング加振機構で加振したときの，薄板の時系列変位をレーザ変位計にて測定したデータが，図1に黒丸●でプロットされています．これに対して，式(1)を当てはめることで $A$ ， $\gamma$ ， $\omega$ を推定します．これを，測定波形のフィッティングと呼んでいます．この結果，

$A=0.0013\;\;{\rm m}$ ， $\gamma =102\;\;{\rm s^{-1}}$ ， $\omega =360\;\;{\rm rad\!/s}$

となります．薄板の時系列変位に対しまして，式(1)をフィッティングしたグラフを図1に赤線で示します．

図1: モデル1のフィッティング

モデル2:角振動数が変動する減衰波

モデル1のフィッティング結果を見ますと，1周期目の後半に入りますあたりから，モデル波形と計測波形のずれが大きくなっていることがわかります．そこで，角振動数 $\omega\,$ を定数ではなく時刻 $\,t\,$ の関数 $\omega (t)\,$ としてみます[2]．つまり，

$x(t)=Ae^{-\gamma t}\sin \lbrace \omega (t)t\rbrace$ 　　　(2)

とします．これを微分しまして $\it\Omega (t)=\dot{\omega }(t)t+\omega (t)$ としますと，

$\dot{x}(t)=-\gamma Ae^{-\gamma t}\sin \lbrace \omega (t)t\rbrace +\lbrace \dot{\omega }(t)t+\omega (t)\rbrace Ae^{-\gamma t}\cos \lbrace \omega (t)t\rbrace$

　　　 $\;\;\,=-\gamma x(t)+\it\Omega (t)Ae^{-\gamma t}\cos \lbrace \omega (t)t\rbrace$

となります．これをさらに微分しまして整理しますと，

[+] 途中式を表示する
$\ddot{x}(t)=-\gamma \dot{x}(t)+\dot{\it\Omega }(t)Ae^{-\gamma t}\cos \lbrace \omega (t)t\rbrace$ $-\gamma \it\Omega (t)Ae^{-\gamma t}\cos \lbrace \omega (t)t\rbrace$ $-\lbrace \it\Omega (t)\rbrace ^{2}Ae^{-\gamma t}\sin \lbrace \omega (t)t\rbrace$

　　　 $\;\;\,=\left{ {\Large\frac{\dot{\it\Omega }(t)}{\it\Omega (t)}}-2\gamma \right} \dot{x}(t)$ $+\left[ \gamma \left{ {\Large\frac{\dot{\it\Omega }(t)}{\it\Omega (t)}}-2\gamma \right} +\gamma ^{2}-\lbrace \it\Omega (t)\rbrace ^{2}\right] x(t)$

となり，すべて左辺に移項しますと，

$\ddot{x}(t)-\left{{\Large\frac{\dot{\it\Omega }(t)}{\it\Omega (t)}}-2\gamma \right}\dot{x}(t)$ $-\left[ \gamma \left{{\Large\frac{\dot{\it\Omega }(t)}{\it\Omega (t)}}-2\gamma \right}+\gamma ^{2}-\lbrace \it\Omega (t)\rbrace ^{2}\right] x(t)=0$

という方程式が導かれます．ここで，

$P(t)=-\left{ {\Large\frac{\dot{\it\Omega }(t)}{\it\Omega (t)}}-2\gamma \right}$

$Q(t)=-\left[ \gamma \left{ {\Large\frac{\dot{\it\Omega }(t)}{\it\Omega (t)}}-2\gamma \right} +\gamma ^{2}-\{ \it\Omega (t)\} ^{2}\right]$

とおきますと,

$\ddot{x}(t)+P(t)\dot{x}(t)+Q(t)x(t)=0$

という斉次2階変数係数線形常微分方程式となります．この場合，2つの線形独立な解空間の基底が存在しますので，それらを $x_{1}(t)\,$ ， $x_{2}(t)\,$ とおき，それぞれ上式に代入しますと，

$\ddot{x}_{1}(t)+P(t)\dot{x}_{1}(t)+Q(t)x_{1}(t)=0$ 　　　(3)

$\ddot{x}_{2}(t)+P(t)\dot{x}_{2}(t)+Q(t)x_{2}(t)=0$ 　　　(4)

となります．式(3) $\,\times \,x_{2}(t)\,-\,$ 式(4) $\,\times \,x_{1}(t)$ としまして $Q(t)\,$ を消去しますと，

$\ddot{x}_{1}(t)x_{2}(t)-\ddot{x}_{2}(t)x_{1}(t)+P(t)\left{ \dot{x}_{1}(t)x_{2}(t)-\dot{x}_{2}(t)x_{1}(t)\right} =0$

となります． $x_{1}(t)\,$ ， $x_{2}(t)\,$ が線形独立の場合，ロンスキーの行列式が0でない条件より，

$\dot{x}_{1}(t)x_{2}(t)-\dot{x}_{2}(t)x_{1}(t)\ne 0$

なので，

${\Large\frac{\ddot{x}_{1}(t)x_{2}(t)-\ddot{x}_{2}(t)x_{1}(t)}{\dot{x}_{1}(t)x_{2}(t)-\dot{x}_{2}(t)x_{1}(t)}}=-P(t)$

とすることができまして，計算していきますと，

$\int{{\Large\frac{\ddot{x}_{1}(t)x_{2}(t)-\ddot{x}_{2}(t)x_{1}(t)}{\dot{x}_{1}(t)x_{2}(t)-\dot{x}_{2}(t)x_{1}(t)}}dt}$ $=-\int{P(t)dt}=\int{\left{ {\Large\frac{\dot{\it\Omega }(t)}{\it\Omega (t)}}-2\gamma \right} dt}$

対数微分法より，

$\log \left| \dot{x}_{1}(t)x_{2}(t)-\dot{x}_{2}(t)x_{1}(t)\right| =\log \left| \it\Omega (t)\right| -2\gamma t+B$

$\log \left| \dot{x}_{1}(t)x_{2}(t)-\dot{x}_{2}(t)x_{1}(t)\right|=\log \left|\it\Omega (t)\,e^{-2\gamma t}\,e^{B}\right|$

$\left|\dot{x}_{1}(t)x_{2}(t)-\dot{x}_{2}(t)x_{1}(t)\right| =e^{B}\,e^{-2\gamma t}\left|\it\Omega (t)\right|$ ．

$\dot{x}_{1}(t)x_{2}(t)-\dot{x}_{2}(t)x_{1}(t)$ と $\it\Omega(t)$ が正の場合， $C=e^B$ として ${\left{x_1(t)\right}}^2$ で両辺をわると，

${\Large\frac{\dot{x}_{1}(t)x_{2}(t)-\dot{x}_{2}(t)x_{1}(t)}{\left{ x_{1}(t)\right} ^{2}}}={\Large\frac{C}{\left{ x_{1}(t)\right} ^{2}}}\it\Omega (t)e^{-2\gamma t}$ ．

よって，分数関数の微分法より，

$-{\Large\frac{d}{dt}\left{ \frac{x_{2}(t)}{x_{1}(t)}\right}} ={\Large\frac{C}{\left{ x_{1}(t)\right} ^{2}}}\it\Omega (t)e^{-2\gamma t}$

となります． $\dot{x}_{1}(t)x_{2}(t)-\dot{x}_{2}(t)x_{1}(t)$ や $\it\Omega(t)$ が負の場合も同じ形となります．解空間の基底の1つは式(2)ですから，

$x_{1}(t)=Ae^{-\gamma t}\sin \left{ \omega (t)t\right}$

としますと，

[+] 途中式を表示する
${\Large\frac{x_{2}(t)}{x_{1}(t)}}=-{\Large\int{\frac{C}{\left[ Ae^{-\gamma t}\sin \left{ \omega (t)t\right} \right] ^{2}}}}\it\Omega (t)e^{-2\gamma t}dt$

${\Large\frac{x_{2}(t)}{x_{1}(t)}}=-{\Large\frac{C}{A^{2}}\int{\frac{\frac{d}{dt}\left{ \omega (t)t\right} }{\sin ^{2}\left{ \omega (t)t\right}}}}dt$

となります．ここで $u=\omega (t)\,t$ としまして計算していきますと，

[+] 途中式を表示する
${\Large\frac{x_{2}(t)}{x_{1}(t)}}=-{\Large\frac{C}{A^{2}}\int{\frac{1}{\sin ^{2}u}}}du$

$x_{2}(t)={\Large\frac{Cx_{1}(t)}{A^{2}\tan \left{ \omega (t)t\right} }}+C'x_{1}(t)$

　　　　 $\;={\Large\frac{C}{A}}\,e^{-\gamma t}\cos \left{ \omega (t)t\right} +C'Ae^{-\gamma t}\sin \left{ \omega (t)t\right}$

となります．したがって一般解は，

[+] 途中式を表示する
$x(t)=x_{1}(t)+x_{2}(t)$

　　　 $\;\,=\sqrt{(A')^{2}+(B')^{2}}e^{-\gamma t}\sin \left{ \omega (t)t+\theta \right}$

$A^{'}=A+C'A$ ， $B'={\Large\frac{C}{A}}$ ， $\cos \theta ={\Large\frac{A'}{\sqrt{(A')^{2}+(B')^{2}}}}$ ， $\sin \theta ={\Large\frac{B'}{\sqrt{(A')^{2}+(B')^{2}}}}$

となります．

実際にハンマリング加振機構で加振したときの薄板の時系列変位に対しまして，角振動数自身が角振動数 $\omega _{2}$ で周期的に変動するとして，

$\omega (t)=\omega _{1}(1-e^{-\gamma t}\sin \omega _{2}t)$

としまして，式(2)をフィッティングしますと，

$A=0.0013\;\;{\rm m}$ ， $\gamma =95\;\;{\rm s^{-1}}$ ， $\omega_1 =360\;\;{\rm rad\!/s}$ ， $\omega_2 =60\;\;{\rm rad\!/s}$

となります．薄板の時系列変位に対しまして，式(2)をフィッティングしたグラフを図2に示します．

図2: モデル2のフィッティング

モデル3:複数の減衰波の重ね合わせ

薄板が加振されまして振動するとき，薄板の端からの反射波による振動や薄板以外の部分の振動など，複数の振動が重なっている可能性があります．そこでモデル3は，複数の減衰波を重ね合わせまして，

$x(t)=\sum_{i=1}^{N}{A_{i}\:e^{-\gamma _{i}\:t}\sin (\omega _{i}\:t+\theta _{i})}$ 　　　(5)

としました[3]．実際にハンマリング加振機構で加振したときの薄板の変位波形に対しまして， $N=4$ としまして式(5)をフィッティングしますと，

$A_1$ ≒ $2.96\;\;{\rm m}$ ， $\;\;\;\;\;\;\;\;\;\;\,\gamma_1$ ≒ $276\;\;{\rm s^{-1}}$ ， $\;\;\;\,\omega_1$ ≒ $347\;\;{\rm rad\!/s}$ ， $\theta_1$ ≒ $0.0721\;\;{\rm rad\!/s}$

$A_2$ ≒ $0.658\;\;{\rm m}$ ， $\;\;\;\;\;\,\gamma_2$ ≒ $228\;\;{\rm s^{-1}}$ ， $\;\;\;\,\omega_2$ ≒ $760\;\;{\rm rad\!/s}$ ， $\theta_2$ ≒ $-3.14\;\;{\rm rad\!/s}$

$A_3$ ≒ $0.302\;\;{\rm m}$ ， $\;\;\;\;\;\gamma_3$ ≒ $52.8\;\;{\rm s^{-1}}$ ， $\,\omega_3$ ≒ $418\;\;{\rm rad\!/s}$ ， $\theta_3$ ≒ $-2.36\;\;{\rm rad\!/s}$

$A_4$ ≒ $0.0668\;\;{\rm m}$ ， $\gamma_4$ ≒ $44.9\;\;{\rm s^{-1}}$ ， $\omega_4$ ≒ $978\;\;{\rm rad\!/s}$ ， $\theta_4$ ≒ $-3.14\;\;{\rm rad\!/s}$

となります．ただしこれらの値は，互いに独立なものとしてフィッティングしました．薄板の時系列変位に対しまして，式(5)をフィッティングしたグラフを図3に示します．

図3: モデル3のフィッティング

モデル3はかなりよく計測波形に一致しているように見えます．しかし実際には， $A_i\,$ ， $\gamma_i\,$ ， $\omega_i\,$ ， $\theta_i\,$ は，それぞれ独立した値をとることはできないと思われるため，さらに考慮したモデルを検討しなければならないと考えています．また，各パラメータが示す振動成分が，実際に，何の対象物の振動を反映しているのかを同定することも必要であると考えています．