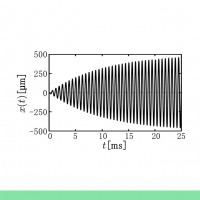
振動現象を簡単な微分方程式で表現する!?
和田先生
前回は,中学校で登場する「二次方程式」のお話をしました.忘れていた方は思い出していただけましたか.肩慣らしとなりましたでしょうか.
第2回は,振動現象を簡単な微分方程式で表してみたいと思います.こっしー君は数学が得意でしたので,道案内をお願いします.
第2回は,振動現象を簡単な微分方程式で表してみたいと思います.こっしー君は数学が得意でしたので,道案内をお願いします.
和田先生
はい,ありがとうございます.
これを解けばいいのですが,今は,外力) は0としましょう.
は0としましょう.
ゆっくりでいいので解いていってください.
これを解けばいいのですが,今は,外力
ゆっくりでいいので解いていってください.
和田先生
数学的には,解の存在を示す必要がありますが,ここでは存在するとし,その解は線形独立な2つの解空間の基底(基本解)で構成されることを使います.要するに,比例関係にない2つの基本解の定数倍を含む和で表せることを既知とするというわけです.すなわち, および
および が基本解だとするとき,定数を
が基本解だとするとき,定数を および
および とし,解は,
とし,解は,
と表せることを使います.
次回は,この微分方程式を解いてみましょう.
この記事と合わせて読みたいページ
和田先生のプロフィール

TMCシステムの研究責任者.電子情報通信学会の会員.
電気接点の劣化現象などに関する論文を多数執筆.
プライベートでは,ギター演奏・料理・読書と幅広い趣味を持つ.
こっしー君のプロフィール

TMCシステムの研究担当者.電子情報通信学会の会員.
得意分野は数学と機械工学.
趣味は読書.特技はペン習字.