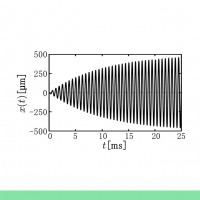
自由振動
和田先生
そうです.
そして,
そして,
(Ⅰ) のときは,過減衰となり,無周期運動,
(Ⅱ) のときは,臨界減衰となり,同じく,無周期運動でしたが,
(Ⅲ) のときは,減衰周期運動となり,この場合が最もよく目にする振動現象を表していました.
私たちは,この(Ⅲ)の場合に注目してお話を続けることにしましょう.
(Ⅲ)の場合の式(7)で表されている振動は,減衰自由振動とよばれています.
振動現象の,自己
和田先生
「自由」という言葉が冠されていますが,これは,考えている「系(system)」

に外力が作用しないという意味として使っています.
従って,起こる振動に関係するもの,これをパラメータと呼んでいますが,これが系内のものに限定されていることになります.
平たく言えば,系自身に固有の力学的性質にのみ左右される振動であるということです.その意味では「振動現象の自己」というように呼んでもいいのではないでしょうか.
こっしー君
「系自身に固有の力学的性質」とは,何でしょうか.
こっしー君
わかりました.忘れないようにし,また,よく理解していきたいと思います.
ところで,今回は「振動現象の,自己と他者」という題目になっていますが,どのような展開になっていくのでしょうか.
和田先生
それでは,それについて次回お話しましょう.
この記事と合わせて読みたいページ
和田先生のプロフィール

TMCシステムの研究責任者.電子情報通信学会の会員.
電気接点の劣化現象などに関する論文を多数執筆.
プライベートでは,ギター演奏・料理・読書と幅広い趣味を持つ.
こっしー君のプロフィール

TMCシステムの研究担当者.電子情報通信学会の会員.
得意分野は数学と機械工学.
趣味は読書.特技はペン習字.