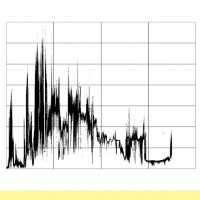
時系列波形のグラフ
共通して言えることは,初期のうちは(15-20 msあたりまで),式(80)の第2項にあたる自由振動項がみられますが,後半以降では減衰して見られなくなります.
ところが,(Ⅲ)の場合は,さらに様子が異なり,前半で大きく振幅が増加していくところが見て取れます.
これは,共振現象と呼ばれており, のとき外力の角振動数
と固有角振動数
が近くなったときにおこる現象です.
式(65)より,この現象に焦点を当てて描いたのが共振曲線と呼ばれているものです(下図).

が小さい場合,
で鋭いピークが現れ,その前後で急激に減少するという特徴を示します.
共振現象は電流などにも生じ,うまく使えばラジオの同調回路のように,小さい信号を大きくすることができます.また,楽器の弦の調音に音叉を使うときも,この現象を利用できます.他方,機械装置や建造物などのように,できるだけ共振を避けたい場合もあります.
と
が近づいてくると,他者のアプローチに対して,自己が敏感に反応し始めていることがうかがわれます.自己のこころに激しい動揺が広がっている状態でしょうか.こうなってくると,この動揺は隠しきれません.
そういえば,百人一首のなかに,
・忍ぶれど 色に出でにけり 我が恋は 物や思ふと 人の問ふまで
[第40首/平兼盛]
・恋すてふ わが名はまだき 立ちにけり 人知れずこそ 思ひそめしか
[第41首/壬生忠見]
なんて和歌がありましたっけ.
なんだか,文学的・心理学的な解析をしているように思えてきますね.
今回は,この辺にしておきましょう.
次回は,外力が周期関数ですが,正弦波の単純な組み合わせでは表せない場合についてお話しいたします.
最も簡単な方法は,フーリエ級数展開によって外力波形を表現する方法です.
この記事と合わせて読みたいページ
和田先生のプロフィール

TMCシステムの研究責任者.電子情報通信学会の会員.
電気接点の劣化現象などに関する論文を多数執筆.
プライベートでは,ギター演奏・料理・読書と幅広い趣味を持つ.
こっしー君のプロフィール

TMCシステムの研究担当者.電子情報通信学会の会員.
得意分野は数学と機械工学.
趣味は読書.特技はペン習字.
※記事の内容に関するご質問などがございましたら、お問い合わせからご連絡いただくか、もしくはコメント欄↓にご記入いただければと思います。後日、担当者よりご連絡させていただきます。