判別式が意味するもの!?
和田先生
今回と次回で「二次方程式」の判別式が意味するものについて考えていきます.
まず,二次方程式のところで注目した判別式を考えます.判別式によって,現れる振動の性質が区別できます.機械的な振動現象は,中学校で学習する二次方程式で説明できるというわけです.すごいですね.
こっしー君,お願いします.
こっしー君
はい,では,進めます.
(Ⅰ) のとき
,
,
が正であることから,
は式(5)より正または0なので
.
このとき,一般解は,
. (11)
ここで,初期条件を用いると,
,
(12)
となるので,特殊解は,
(13)
または,
(14)
となります.
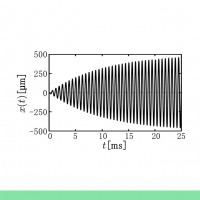
変位の時間変化を図に示します.これは無周期運動で,過減衰と呼んでいます.今回示す3つの中で最も減衰が大きい場合です.

(Ⅱ) のとき
式(8)をもう一度書きます.
初期条件より,
,
. (15)
よって,特殊解は,
となります.
変位の時間変化を図に示します.これも無周期運動で,臨界減衰と呼んでいます.(Ⅰ)の過減衰と次に示す(Ⅲ)減衰周期運動の境界にあたります.

和田先生
こっし―君、ありがとうございます。
今回は,少し長くなりましたので,この辺で次回に回したいと思います.
話の続きを少し想像してみてください.指数関数と三角関数の不思議な結びつきのお話になると思います.
今回は,少し長くなりましたので,この辺で次回に回したいと思います.
話の続きを少し想像してみてください.指数関数と三角関数の不思議な結びつきのお話になると思います.
この記事と合わせて読みたいページ
和田先生のプロフィール

TMCシステムの研究責任者.電子情報通信学会の会員.
電気接点の劣化現象などに関する論文を多数執筆.
プライベートでは,ギター演奏・料理・読書と幅広い趣味を持つ.
こっしー君のプロフィール

TMCシステムの研究担当者.電子情報通信学会の会員.
得意分野は数学と機械工学.
趣味は読書.特技はペン習字.