【和田先生のなるほどゼミナール5】振動現象をつむぐ，中学校の数学5

判別式が意味するもの！？

和田先生

$D\gt0$ のとき 過減衰，

$D=0$ のとき 臨界減衰，となることをお話ししました．

今回はいよいよ，振動現象が現れるお話です．
$D\lt0$ のときは，二次方程式で解が実数でない複素数のときでした．二次方程式における複素数解については，直感的に理解するのが少し難しいと思います．かろうじて二次関数の性質を説明するときに役立ちますが．ところが，実際の振動論で最もよくあらわれるケースがこの複素数解のときなのです．少し不思議ですね．

では，主役の登場です．
こっしー君，よろしくお願いします．

こっしー君

では説明します．

(Ⅲ) $D\lt0$ のとき

このときは，すなわち，

$0\lt\zeta\lt1$

のときで，一般解は，前回の式(10)と同じで，

$x(t)=Ae^{\left(-\zeta+\sqrt{\zeta^{2}-1}\right)\omega_{0}t}+Be^{\left(-\zeta-\sqrt{\zeta^{2}-1}\right)\omega_{0}t}$ (16)

となります．

ここで， $\sqrt{\;\;\;$ の中が負なので，虚数単位 $i$ を用いて表現方法を変えます．

すなわち，

$\sqrt{\zeta^{2}-1}=i\sqrt{1-\zeta^{2}$

とします．

虚数単位は，

$i^{2}=-1$

です．不思議な世界に入っていく感じがします．

式(16)より，

$x(t)=Ae^{\left(-\zeta+i\sqrt{1-\zeta^{2}}\right)\omega_{0}t}+Be^{\left(-\zeta-i\sqrt{1-\zeta^{2}}\right)\omega_{0}t}$

$x(t)=Ae^{-\zeta\omega_{0}t}e^{i\sqrt{1-\zeta^{2}}\omega_{0}t}+Be^{-\zeta\omega_{0}t}e^{-i\sqrt{1-\zeta^{2}}\omega_{0}t}$ . (17)

ちょっと困りました．

$e^{i\sqrt{1-\zeta^{2}}\omega_{0}t}$ や $e^{-i\sqrt{1-\zeta^{2}}\omega_{0}t}$

はどうしたらいいのでしょう．

オイラーの公式：指数関数から三角関数が出てくる！？

和田先生

これは，オイラーの公式と呼ばれているものを用います．
すなわち任意の $\theta$ に対する，

$e^{i\theta }=\cos \theta +i\sin \theta$ (18)

を用います．
この公式は不思議な魅力のある式で，色々な方法で証明が試みられています．数学の一般書やウェブサイト（Wikipediaなど）を見てください．

この公式が最も不思議なのは， $\pi$ を円周率として，

$\theta =\pi$

を代入したときです．そうすると，式(18)は，

$e^{i\pi }=-1$ (19)

$e^{i\pi }+1=0$ (20)

となります．

数学で出てくる，重要でかつ不思議な無理数 $e$ と $\pi$ ，先ほど出てきた虚数単位 $i$ ，および最も身近な整数 $0$ (加法に関する単位元，すなわち零元)と $1$ (乗法に関する単位元)が出てきて，それらが単純な等式で結ばれています．
数学は発見なのか発明なのかの議論がありますが，この式を見ていると発見だと思いたくなります．

少し横道に逸れました．
このオイラーの公式(18)を用いると

$e^{i\sqrt{1-\zeta^{2}}\omega_{0}t}=\cos \sqrt{1-\zeta^{2}}\omega_{0}t+i\sin \sqrt{1-\zeta^{2}}\omega_{0}t$ (21)

$e^{-i\sqrt{1-\zeta^{2}}\omega_{0}t}=\cos \sqrt{1-\zeta^{2}}\omega_{0}t-i\sin \sqrt{1-\zeta^{2}}\omega_{0}t$ (22)

となります．
続けてください．

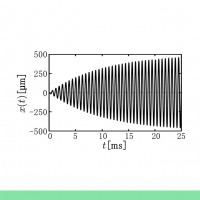
振動現象をつむぐ，虚数単位！？

こっしー君

式(21)と式(22)より,式(17)は，

$x(t)=Ae^{-\zeta\omega_{0}t}\left(\cos \sqrt{1-\zeta^{2}}\omega_{0}t+i\sin \sqrt{1-\zeta^{2}}\omega_{0}t\right)$

$+Be^{-\zeta\omega_{0}t}\left(\cos \sqrt{1-\zeta^{2}}\omega_{0}t-i\sin \sqrt{1-\zeta^{2}}\omega_{0}t\right)$

$=(A+B)e^{-\zeta\omega_{0}t}\cos \sqrt{1-\zeta^{2}}\omega_{0}t+i(A-B)e^{-\zeta\omega_{0}t}\sin \sqrt{1-\zeta^{2}}\omega_{0}t$

$=e^{-\zeta\omega_{0}t}\left(\tilde{A}\cos \sqrt{1-\zeta^{2}}\omega_{0}t+\tilde{B}\sin \sqrt{1-\zeta^{2}}\omega_{0}t\right)$ . (23)

ここで，

$\tilde{A}=A+B$ , $\tilde{B}=i(A-B)$ . (24)

式(23)に初期条件を用いると，

$x_{0}=\tilde{A}$ , $v_{0}=-\zeta\omega_{0}\tilde{A}+\sqrt{1-\zeta^{2}}\omega_{0}{B}$ (25)

となり，

$\left[\begin{array}{cc}x_{0} \\ v_{0} \end{array}\right] =\left[\begin{array}{cc}1 & \;\;\;0 \\ -\zeta\omega_{0} & \;\;\;\sqrt{1-\zeta^{2}}\omega_{0} \end{array}\right]$ $\left[\begin{array}{cc}\tilde{A} \\ \tilde{B} \end{array}\right]$

$\left[\begin{array}{cc}\tilde{A} \\ \tilde{B} \end{array}\right] =\frac{1}{\sqrt{1-\zeta^{2}}\omega_{0}}$ $\left[\begin{array}{cc}\sqrt{1-\zeta^{2}}\omega_{0} & \;\;\;0 \\ \zeta\omega_{0} & \;\;\;1 \end{array}\right] \left[\begin{array}{cc}x_0 \\ v_0 \end{array}\right]$ .

すなわち，

$\tilde{A}=x_{0}$ , $\tilde{B}=x_{0}\frac{\zeta+\frac{v_{0}}{x_{0}\omega_{0}}}{\sqrt{1-\zeta^{2}}}$ . (26)

和田先生

あれ，式(26)を見ると， $\tilde{A}$ と $\tilde{B}$ は実数になっています．
ところが， $\tilde{A}$ と $\tilde{B}$ は式(24)で定義されています．
この式では， $\tilde{B}$ が虚数になっているように見えて気持ち悪いですね．

こっしー君

それは，実際に計算してみると解決します．

式(24)より，

$\left[\begin{array}{cc}\tilde{A} \\ \tilde{B} \end{array}\right] =\left[\begin{array}{cc}1 & \;\;\;1 \\ i & \;\;\;-i \end{array}\right] \left[\begin{array}{cc}{A} \\ {B} \end{array}\right]$

$\left[\begin{array}{cc}A \\ B \end{array}\right] =\frac{1}{-2i}\left[\begin{array}{cc}-i & \;\;\;-1 \\ -i & \;\;\;1 \end{array}\right]$ $\left[\begin{array}{cc}\tilde{A} \\ \tilde{B} \end{array}\right]=\frac{1}{2}\left[\begin{array}{cc}\tilde{A}-i\tilde{B} \\ \tilde{A}+i\tilde{B} \end{array}\right]$ .

$\tilde{A}$ と $\tilde{B}$ は式(26)より実数なので， ${A}$ と ${B}$ が共役な複素数だったのです．

これより， $A+B$ が実数， $A-B$ が純虚数となるので， $\tilde{B}$ は実数になります．結構きわどい気がしますが．

和田先生

よかった．
続けてください．

こっしー君

式(23)と(26)より，三角関数の合成を行います.

$x(t)=e^{-\zeta\omega_{0}t}(\tilde{A}\cos \sqrt{1-\zeta^{2}}\omega_{0}t+\tilde{B}\sin \sqrt{1-\zeta^{2}}\omega_{0}t)$

$=x_{0}e^{-\zeta\omega_{0}t}\left(\cos \sqrt{1-\zeta^{2}}\omega_{0}t+\frac{\zeta+\frac{v_{0}}{x_{0}\omega_{0}}}{\sqrt{1-\zeta^{2}}}\sin \sqrt{1-\zeta^{2}}\omega_{0}t\right)$

$=ae^{-\zeta\omega_{0}t}\cos \left(\sqrt{1-\zeta^{2}}\omega_{0}t-\beta\right)$

ここで,

$\frac{a}{x_{0}}=\sqrt{\frac{1+2\zeta\frac{v_{0}}{x_{0}\omega_{0}}+\left(\frac{v_{0}}{x_{0}\omega_{0}}\right)^{2}}{1-\zeta^{2}}}$ , $\tan\beta =\frac{\zeta+\frac{v_{0}}{x_{0}\omega_{0}}}{\sqrt{1-\zeta^{2}}}$