振動現象の,自己と他者
和田先生
今回は,式(1)において,) が0でない場合についてのお話です.
が0でない場合についてのお話です.
今までの話は,外力 がない場合のお話で,
いわば「振動現象の,自己」にあたることでした.
今回は が0でない場合についてのお話でして,
いわば「振動現象の,自己と他者」にあたることになります.
こっしー君
「自己と他者」!
この言葉は,聞いたことがあります.
確か,R.D.レインの『自己と他者』(みすず書房 1975)という著作があったように記憶しています.
この言葉は,聞いたことがあります.
確か,R.D.レインの『自己と他者』(みすず書房 1975)という著作があったように記憶しています.
和田先生
そうですね.
R.D.レインは,イギリスの医学者・精神科医・精神分析家でして,その著作の一つが『自己と他者』です.興味があったら読んでみてください.
R.D.レインに興味がある人は,著作を読むのが一番ですが,Webでも色々解説されていますよ.
ここでは,
「他者の言動からの影響は,ほぼ全ての人が避けられない.」
という意味を込めています.
R.D.レインは,イギリスの医学者・精神科医・精神分析家でして,その著作の一つが『自己と他者』です.興味があったら読んでみてください.
R.D.レインに興味がある人は,著作を読むのが一番ですが,Webでも色々解説されていますよ.
ここでは,
「他者の言動からの影響は,ほぼ全ての人が避けられない.」
という意味を込めています.
こっしー君
「系」は外力が0でない場合は,その振動現象は外力の影響を受ける,ということでしょうか.
強制振動
こっしー君
どういたしましょう.
和田先生
より一般的な解法として,「定数変化法」という解法があります(ご要望があれば解説いたします.)が,計算が少し煩雑です.
我々は,まずは,外力) として初等的なものを対象とするので,「未定係数法」というより簡単な方法で解いてみましょう.
として初等的なものを対象とするので,「未定係数法」というより簡単な方法で解いてみましょう.
我々は,まずは,外力
こっしー君
未定係数法!
でもそれは,) が具体的な関数でないとできないような気がします.
が具体的な関数でないとできないような気がします.
でもそれは,
和田先生
そうです.
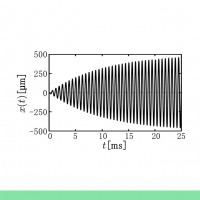
そこで,振動試験機などでよく用いられている周期的外力の関数として,三角関数,sinを用いようと思います.
すなわち,
そこで,振動試験機などでよく用いられている周期的外力の関数として,三角関数,sinを用いようと思います.
すなわち,
とします.これで,式(1)の代わりに,
を考えます.ここで, は周期的外力の角振動数です.この周期
で外力は周期変動をします.
さあ,どうしましょうか.
特殊解:)
こっしー君
こっしー君
でも,やっぱり,) はわかりませんよね.
はわかりませんよね.
この記事と合わせて読みたいページ
和田先生のプロフィール

TMCシステムの研究責任者.電子情報通信学会の会員.
電気接点の劣化現象などに関する論文を多数執筆.
プライベートでは,ギター演奏・料理・読書と幅広い趣味を持つ.
こっしー君のプロフィール

TMCシステムの研究担当者.電子情報通信学会の会員.
得意分野は数学と機械工学.
趣味は読書.特技はペン習字.