微分方程式を解く!?:一般解
和田先生
こっしー君
わかりました.
 を未知数,
を未知数, を自然対数の底として,前回導いた微分方程式
を自然対数の底として,前回導いた微分方程式
(4)
の解を仮に,
としてみると,
,
.
これらを,式(4)に代入すると,
.
が有限の時は,
なので,割ることができて,
となります.
ここに,「振動現象をつむぐ,中学校の数学1」に出てきた,「二次方程式」が出てきました.
和田先生
そうですね.
では解いていってください.
では解いていってください.
こっしー君
線形微分方程式の一般解:微分方程式にも二次方程式の香りが?
 のときの一般解
のときの一般解
 のときの一般解
のときの一般解
和田先生
では,次に,
の場合について調べてください.
和田先生
これで,微分方程式の一般解が求められました.
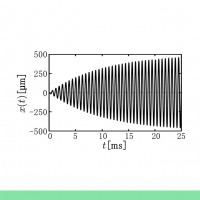
初期値を代入することで特殊解が求められ,振動の姿が描き出せることになります.
初期値を代入することで特殊解が求められ,振動の姿が描き出せることになります.
次回は,いよいよ,「二次方程式」の判別式が意味するものについて考えてみましょう.
この記事と合わせて読みたいページ
和田先生のプロフィール

TMCシステムの研究責任者.電子情報通信学会の会員.
電気接点の劣化現象などに関する論文を多数執筆.
プライベートでは,ギター演奏・料理・読書と幅広い趣味を持つ.
こっしー君のプロフィール

TMCシステムの研究担当者.電子情報通信学会の会員.
得意分野は数学と機械工学.
趣味は読書.特技はペン習字.