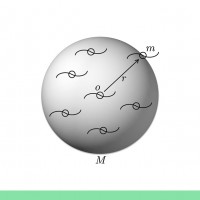
ドップラー赤方偏移とは


および
は光の波の周期と等しい時間とします.
図は光源と同速度の座標系を示しています.
図の緑の実線は観測者の位置を示しており, 軸からの傾きはこの座標系に対して相対速度
を持っていることを表します.
図では,光源が観測者から見て負の方向にあり, が正ですので,光源から遠ざかっていることを示しています.
すなわち, です.
光の波の1山目の位置を青の破線で,2山目の位置を赤の破線で示しています.
図より,
よって,
さらに,
観測者とともに運動する系では,ローレンツ変換されて,
また,式(9)および(10)より時間成分で考えると,
観測者にとっては,光の波の1山目が到達してから2山目が到達するまでの時間が,光の波の周期 となるので,
よって,
となります.
ちなみに,途中計算は省きますが,ローレンツ変換後の座標系,つまり観測者と同速度の座標系では,以下のような図になります.

ありがとうございます.
ハッブルの法則
ほとんど全ての銀河のスペクトルに赤方偏移が見られること,
および,
赤方偏移の量は遠方の銀河ほど大きいこと
を発見しました.
これを「ハッブルの法則」と呼んでいます.
天体の相対速度(後退速度)を ,ハッブル定数を
,その天体までの距離を
とすると,
ハッブル定数は,次元は [ T ] で,
単位としては便宜上,
] が用いられます.
2014年の時点で,最も正確な値は、プランクの観測による
67.15±1.2
だそうです.
(Planck Reveals an almost perfect universe:European Space Agency).
この「ハッブル定数」が,【和田先生のなるほどゼミナール16】わたしたちの宇宙のみじめな最期5で出した宿題,
宇宙のお話をするときに,欠くことのできない重要な物理定数がもう一つあります.
この定数は, [ T ] で表せます.
その定数とはなんでしょうか.
の解答になります.
ハッブル定数は,我々の宇宙そのものだといわれることもあります.
この事象は、銀河を出た光が地球に届くまでの間に,空間自体が伸びて波長が引き伸ばされるためであると解釈でき,宇宙が膨張していることを示すと考えられています.
我々の宇宙が膨張しているのなら,その時間を遡行していくと,宇宙には「はじまり」があったということになりますね.
現代宇宙論は,今,大変に面白い時期に来ているようです.
ハッブル定数の話の前に,ちょっと,脱線します.「時間を遡行していく」という言葉に引っかかりました.
よく使われる表現としては,「タイム・トラベル」ですね.
この分野の作品は,小説・映画・TVドラマ・コミック・アニメ・ゲームと多岐にわたっており,今回のゼミではとても総括できるスペースはありませんが,気になったものだけ次回,触れてみたいと思います.
いつかこれらの分野を総括できればと考えています.
【問題】
タイムトラベル作品の金字塔「バック・トゥ・ザ・フューチャー」という映画作品のPART2では,主人公が30年後の未来にタイムトラベルします.
さて,その30年後の未来とは西暦何年でしょうか?
①2015年
②2020年
③2025年
次回はこのお話から始めることにしましょう.
この記事と合わせて読みたいページ
和田先生のプロフィール

TMCシステムの研究責任者.電子情報通信学会の会員.
電気接点の劣化現象などに関する論文を多数執筆.
プライベートでは,ギター演奏・料理・読書と幅広い趣味を持つ.
こっしー君のプロフィール

TMCシステムの研究担当者.電子情報通信学会の会員.
得意分野は数学と機械工学.
趣味は読書.特技はペン習字.
※記事の内容に関するご質問などがございましたら、お問い合わせからご連絡いただくか、もしくはコメント欄↓にご記入いただければと思います。後日、担当者よりご連絡させていただきます。